Análisis Exploratorio de Datos en Minería
El análisis exploratorio de datos (EDA) es un paso fundamental en la evaluación de yacimientos mineros. Permite familiarizarse con los datos recolectados, resumir información clave, y verificar la calidad y representatividad de los datos. Este artículo profundiza en los conceptos y métodos utilizados en el EDA dentro del contexto de la minería, destacando su importancia y las técnicas empleadas.
Objetivos del Análisis Exploratorio de Datos
El objetivo principal del EDA es proporcionar una comprensión inicial de los datos antes de aplicar técnicas más sofisticadas de análisis y modelado. Los objetivos específicos incluyen:
- Familiarizarse con los datos.
- Resumir información relevante.
- Desplegar datos para su visualización.
- Seleccionar poblaciones geológicas.
- Definir la zona de estudio.
- Verificar la calidad y representatividad de los datos, identificando duplicados, atípicos, inconsistencias y otros problemas.
Medidas de Posición y Dispersión
Las medidas de posición, como la media, mediana y moda, proporcionan información sobre la centralidad de los datos. Las medidas de dispersión, como la varianza, desviación estándar, rango intercuartil y coeficiente de variación, ofrecen una visión de la variabilidad de los datos.
Ejemplo: Medidas de Posición
- Media: \( \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \)
- Mediana: Valor central de los datos ordenados.
- Moda: Valor más frecuente en el conjunto de datos.
Ejemplo: Medidas de Dispersión
- Varianza: \( s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \)
- Desviación Estándar: \( s = \sqrt{s^2} \)
- Rango Intercuartil: \( IQR = Q3 - Q1 \)
- Coeficiente de Variación: \( CV = \frac{s}{\bar{x}} \)
Análisis de Distribuciones
Las distribuciones de datos pueden proporcionar información crucial sobre la naturaleza de los datos mineros. La distribución normal es una de las más comunes y se define completamente por su media y varianza.
Distribución Normal
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left( \frac{x-\mu}{\sigma} \right)^2} \]
En el contexto minero, también es común encontrar distribuciones lognormales, donde los logaritmos de los datos siguen una distribución normal.
Distribución Lognormal
\[ Y = e^{\mu + \sigma Z} \]
donde \( Z \) es una variable aleatoria con distribución normal estándar.
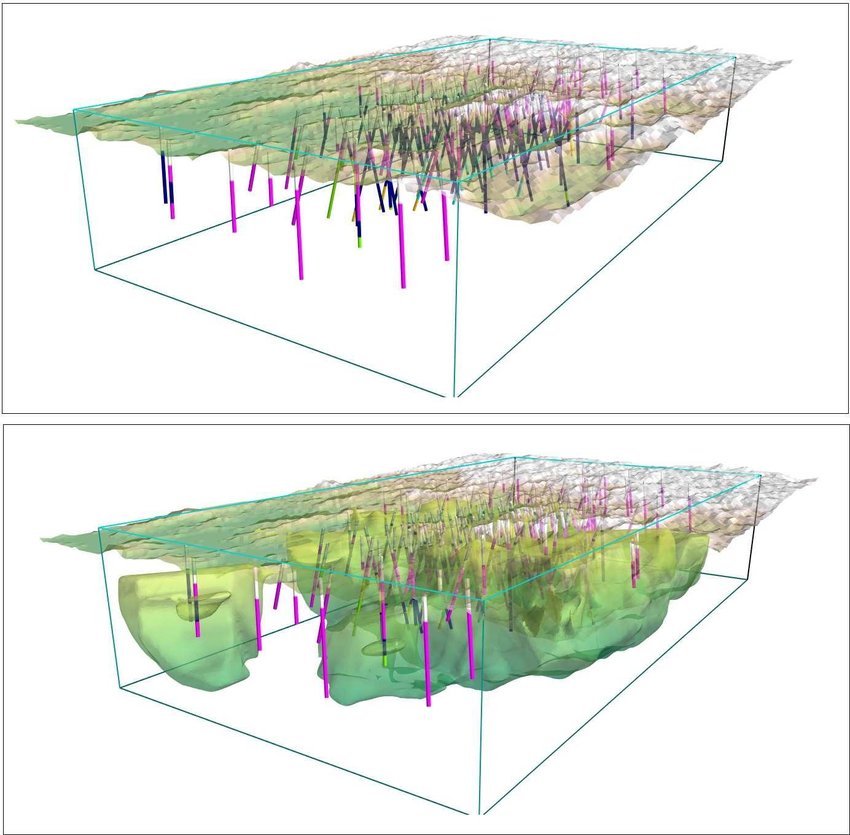
Figura 1: Visualización en 3D de Datos de Sondajes.
Visualización de Datos
La visualización de datos es crucial para el EDA. Gráficos como histogramas, gráficos de caja, y diagramas de dispersión ayudan a identificar patrones, tendencias y anomalías en los datos. La visualización en 3D también es común en la minería para representar la distribución espacial de los datos.
Verificación de la Calidad de los Datos
Verificar la calidad de los datos implica identificar y corregir datos duplicados, atípicos o aberrantes, inconsistencias, y derivas. También incluye evaluar la representatividad de los datos y asegurar que los diferentes tipos de datos disponibles son coherentes y completos.
Proceso de Verificación de Calidad
- Revisión y limpieza de bases de datos.
- Análisis estadístico tradicional.
- Identificación y eliminación de datos anómalos.
- Cálculo de funciones estadísticas espaciales.
Aplicaciones del EDA en Minería
El EDA es esencial para definir la zona de estudio y seleccionar las poblaciones geológicas. También es crucial para el análisis y modelamiento espacial de datos, como la generación de semivariogramas y covariogramas.
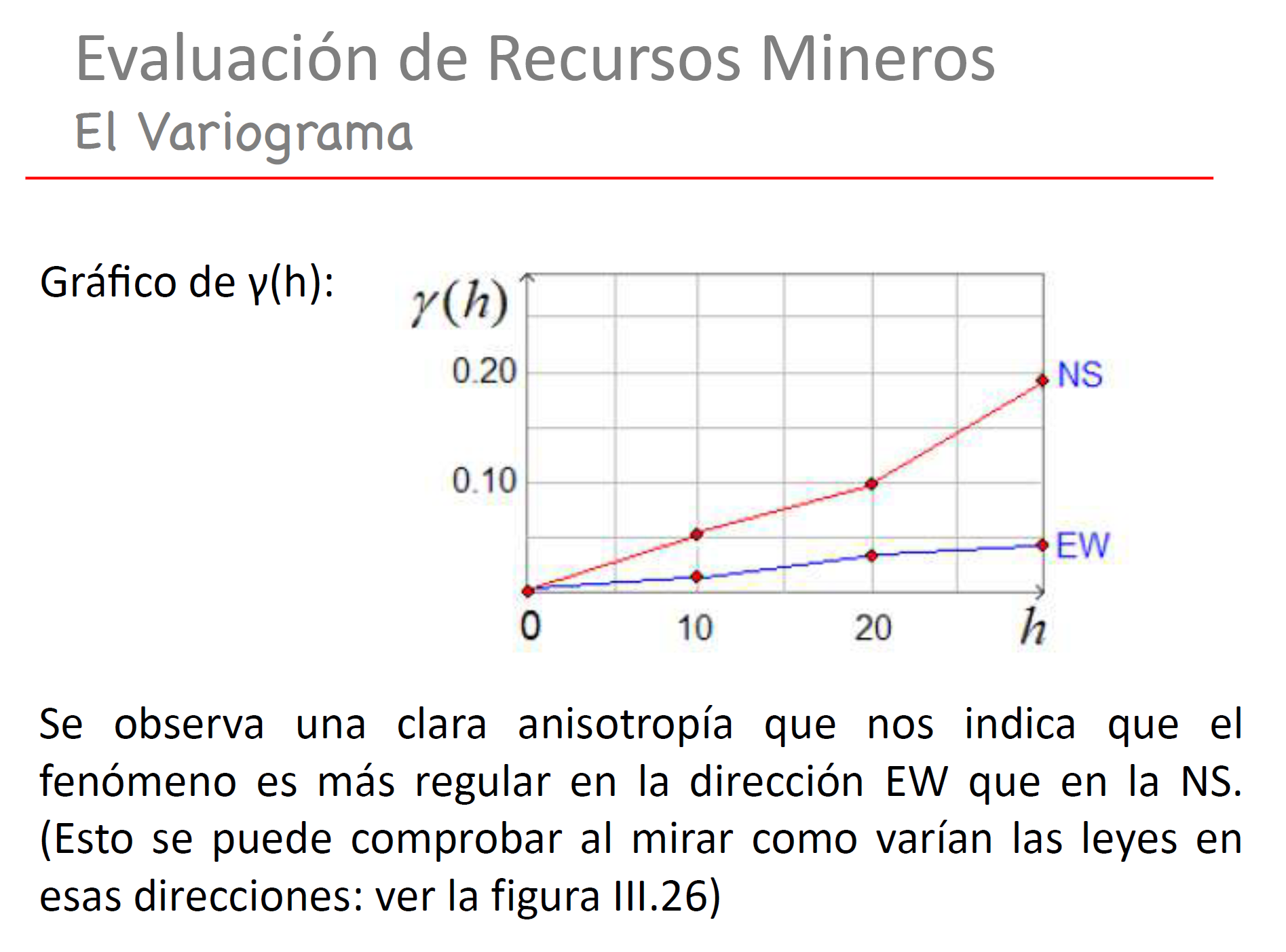
Figura 2: Semivariograma
Conclusión
El análisis exploratorio de datos es una fase crítica en la evaluación de recursos mineros. Proporciona la base para una modelación y estimación precisas, garantizando que los datos utilizados son representativos y de alta calidad. A través de técnicas estadísticas y visualizaciones adecuadas, el EDA ayuda a los geólogos y mineros a comprender mejor la naturaleza y distribución de los recursos minerales.
Referencias
- Journel, A. G., & Huijbregts, C. J. (1978). Mining Geostatistics. Academic Press.
- David, M. (1977). Geostatistical Ore Reserve Estimation. Elsevier Scientific Publishing Company.
- Sinclair, A. J., & Blackwell, G. H. (2002). Applied Mineral Inventory Estimation. Cambridge University Press.
- SME (Society for Mining, Metallurgy, & Exploration). Mining Engineering.
- Informes anuales de BHP y Freeport-McMoRan.

